Use Alloy to model and find a solution to the Goat, Cabbage, and Wolf problem

Introduction

This example uses Alloy to model a system. It is an excellent illustration of the power of Alloy: merely express the constraints and Alloy will find a solution.

A farmer wants to ferry across a river a goat, a cabbage, and a wolf, but his boat only has room for him to take one at a time. If he leaves the goat with the cabbage, the goat will eat it. If he leaves the goat with the wolf, the goat will be eaten. How does the farmer do it?

We will solve the problem by modeling it in Alloy and using the Alloy Analyzer to find a solution.

Constraints

1. Farmer can ferry only one item at a time.
2. Don’t leave the goat and cabbage alone together because the goat will eat the cabbage.
3. Don’t leave the goat and wolf alone together because the wolf will eat the goat.

Solution

Alloy found two solutions. Here is one of them:

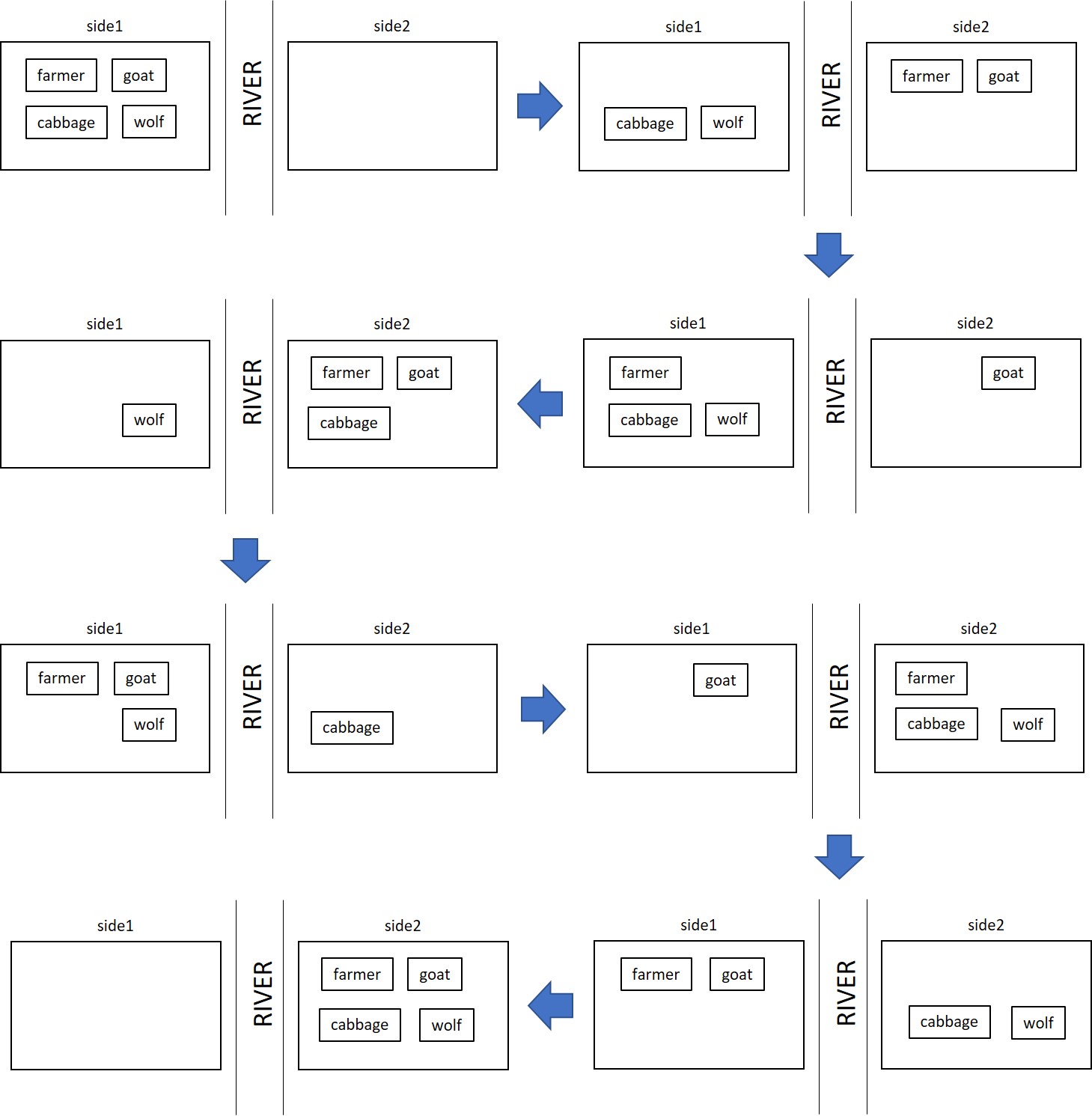
Model of the Farmer -- Goat -- Cabbage -- Wolf System

First, take a snapshot of the system each time the farmer crosses the river. So, the model will contain a series of snapshops. Each snapshot records the items on side1 and side2 of the river. Here is a graphical depiction of one snapshot:

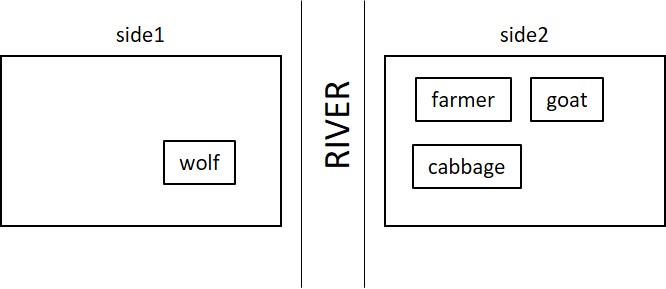
Here’s how to express the set of snapshots:

sig Snapshot {
    side1: set Item,
    side2: set Item
}

The snapshots should be ordered to reflect the fact that there is a first ferry trip, then a second, and so forth. Call the ordering module with the set of snapshots:

open util/ordering[Snapshot]

The term “Item” will be used to denote any of the actors: farmer, goat, cabbage, or wolf. Define a simple classification hierarchy of items:

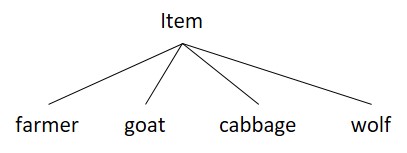
Here’s how to express the hierarchy in Alloy:

abstract sig Item {}
one sig farmer extends Item {}
one sig goat extends Item {}
one sig cabbage extends Item {}
one sig wolf extends Item {}

The initial snapshot—that is, the initial state of the system—has the farmer, goat, cabbage, and wolf on side1 and nothing on side2. That is represented as a “fact” in the model:

fact init {
    first.side1 = farmer + goat + cabbage + wolf
    first.side2 = none
}

The final snapshot must have the farmer, goat, cabbage, and wolf on side2 and nothing on side1. That too is represented as a fact in the model:

fact final {
    some s: Snapshot |
        s.side2 = farmer + goat + cabbage + wolf
        s.side1 = none
}

The following constraints must be satisfied at all time:

• If the farmer is on side1, then the goat and cabbage must not be on side2, and vice versa.
• If the farmer is on side1, then the goat and wolf must not be on side2, and vice versa.

That is represented as a fact in the model:

fact constraints {
    no s: Snapshot { 
        (farmer in s.side1) and (goat + cabbage in s.side2) or
        (farmer in s.side2) and (goat + cabbage in s.side1) or
        (farmer in s.side1) and (goat + wolf in s.side2) or
        (farmer in s.side2) and (goat + wolf in s.side1)
    }
}

There are a series of ferry’s from one side to the other. For each snapshot “s”, if the farmer is on side2 (previously he was on side1), then side2 contains one new item (plus the farmer) and side1 contains one less item (and minus the farmer). That is expressed this way:

farmer in s.prev.side1 => {
    some i: s.prev.side1 - farmer { 
        s.side1 = s.prev.side1 - farmer - i
        s.side2 = s.prev.side2 + farmer + i
    }
}

If the farmer is on side1 (previously he was on side2), then side1 might contain one new item (plus the farmer) and side2 might contains one less item (minus the farmer). Why do I say “might”? Answer: When the farmer returns to side1 he may or may not bring back an item. Here’s how to express this:

farmer in s.prev.side2 => {
    some i: s.prev.side2 - farmer { 
        ((s.side2 = s.prev.side2 - farmer - i) and (s.side1 = s.prev.side1 + farmer + i)) or 
        ((s.side2 = s.prev.side2 - farmer) and (s.side1 = s.prev.side1 + farmer))
    }
}

When we arrive at a snapshot where all the items are on side2, then all following snapshots are unchanged:

goat_cabbage_and_wolf_on_side2 [s.prev] => {
    s.side1 = s.prev.side1
    s.side2 = s.prev.side2
}

This is how “goat_cabbage_and_wolf_on_side2” is defined:

pred goat_cabbage_and_wolf_on_side2 (s: Snapshot) {
    s.side2 = farmer + goat + cabbage + wolf
    s.side1 = none
}

Putting it all together, here’s how the series of ferry trips is modeled:

pred Ferrys_across_river {
    all s: Snapshot - first {
        goat_cabbage_and_wolf_on_side2 [s.prev] => {
            s.side1 = s.prev.side1
            s.side2 = s.prev.side2
        }
        else {
            farmer in s.prev.side1 => {
                some i: s.prev.side1 - farmer { 
                    s.side1 = s.prev.side1 - farmer – i
                    s.side2 = s.prev.side2 + farmer + i
                }
            }
            farmer in s.prev.side2 => {
                some i: s.prev.side2 - farmer { 
                    ((s.side2 = s.prev.side2 - farmer - i) and (s.side1 = s.prev.side1 + farmer + i)) or 
                    ((s.side2 = s.prev.side2 - farmer) and (s.side1 = s.prev.side1 + farmer))
                }
            }
        }
    }
}

By default, Alloy limits the number of members of each set to 3, which means the default is 3 snapshots. The farmer cannot get all the items to side2 in just 3 ferry trips. I bumped up the default to 4 and ran Alloy. No instance found. I bumped it up to 4. No instance found. No instance was found until I bumped up the default to 8:

run Ferrys_across_river for 8

That resulted in Alloy finding two instances. The farmer is able to move all items to side2 in 8 ferry trips.

Complete Alloy Model

open util/ordering[Snapshot]

sig Snapshot {
    side1: set Item,
    side2: set Item
}

abstract sig Item {}
one sig farmer extends Item {}
one sig goat extends Item {}
one sig cabbage extends Item {}
one sig wolf extends Item {}

fact init {
    first.side1 = farmer + goat + cabbage + wolf
    first.side2 = none
}

fact final {
    some s: Snapshot |
    Goat_cabbage_and_wolf_on_side2 [s]
}

fact constraints {
    no s: Snapshot { 
        (farmer in s.side1) and (goat + cabbage in s.side2) or
        (farmer in s.side2) and (goat + cabbage in s.side1) or
        (farmer in s.side1) and (goat + wolf in s.side2) or
        (farmer in s.side2) and (goat + wolf in s.side1)
    }
}

pred goat_cabbage_and_wolf_on_side2 (s: Snapshot) {
    s.side2 = farmer + goat + cabbage + wolf
    s.side1 = none
}

pred Ferrys_across_river {
    all s: Snapshot - first {
        goat_cabbage_and_wolf_on_side2 [s.prev] => {
            s.side1 = s.prev.side1
            s.side2 = s.prev.side2
        }
        else {
            farmer in s.prev.side1 => {
                some i: s.prev.side1 - farmer { 
                    s.side1 = s.prev.side1 - farmer – i
                    s.side2 = s.prev.side2 + farmer + i
                }
            }
            farmer in s.prev.side2 => {
                some i: s.prev.side2 - farmer { 
                    ((s.side2 = s.prev.side2 - farmer - i) and (s.side1 = s.prev.side1 + farmer + i)) or 
                    ((s.side2 = s.prev.side2 - farmer) and (s.side1 = s.prev.side1 + farmer))
                }
            }
        }
    }
}

run Ferrys_across_river for 8